De term "zonsverduistering" is ongelukkig gekozen omdat er eigenlijk niets verduisterd wordt: beter zou zijn "zonsbedekking" of "maanovergang". De traditie heeft echter ook haar rechten en die zullen we hier respecteren.
Een zonsverduistering treedt op wanneer de schaduwkegel van de maan de aarde raakt. Het gebied waar de kernschaduwkegel (groen) van de maan de aarde raakt is typisch een paar honderd kilometer in doormeter, en daar ziet men de zonsverduistering totaal. Rond de kernschaduwvlek is er een veel groter deel van de aarde dat zich in de bijschaduwkegel (rood) van de maan bevindt: daar ziet men de zonsverduistering gedeeltelijk.
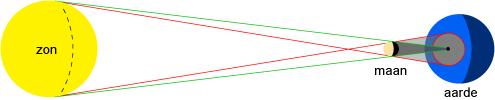
De schaduwkegel van de maan zwiept door de ruimte met dezelfde snelheid als de maan in haar baan om de aarde, namelijk 3700 km/h. De aarde draait terzelfdertijd om haar as in dezelfde zin met een snelheid van 1700 km/h (aan de evenaar), waardoor de schaduw van de maan zich over het aardoppervlak beweegt met een relatieve snelheid van om en bij de 2000 km/h. De tocht van de schaduwkegel van de maan over het aardoppervlak kan verscheidene uren duren.
Types zonsverduisteringen
Het hierboven uiteengezette algemene principe van een zonsverduistering behoeft verdere precisering. Dit leidt tot het indelen van zonsverduisteringen in vier types.



Totale zonsverduistering: Als de kernschaduwkegel van de maan de aarde raakt, spreken we van een totale zonsverduistering. Waar de kernschaduwkegel van de maan de aarde raakt, wordt een totale zonsverduistering als totaal gezien; waar de bijschaduwkegel van de maan de aarde raakt, wordt een totale zonsverduistering als gedeeltelijk gezien. De duur van de totaliteit hangt af van de afstand van de maan: als de maan in de buurt van haar perigeum staat, kan die oplopen tot 7 minuten. Tijdens die totaliteit kan men verschijnselen zien die anders overstraald worden door het felle zonnelicht, zoals protuberansen (zonne-uitbarstingen) en de corona (de zonne-atmosfeer).
Gedeeltelijke zonsverduistering: Als de kernschaduwkegel van de maan de aarde nergens raakt, maar de bijschaduwkegel van de maan wel, spreken we van een gedeeltelijke zonsverduistering. Een gedeeltelijke zonsverduistering wordt dus nergens als totaal gezien!
Ringvormige zonsverduistering: Aangezien de kernschaduwkegel van de maan slecht 375 000 km lang is (vergelijk met de gemiddelde afstand aarde-maan van 384 000 km), zal de kernschaduwkegel van de maan de aarde niet kunnen raken als de maan niet voldoende dicht bij haar perigeum staat. In het verlengde van de kernschaduwkegel ziet men dan de rand van de zonneschijf nog uitsteken rond de (te kleine) maanschijf. Men spreekt dan van een ringvormige zonsverduistering. Waar de bijschaduwkegel van de maan de aarde raakt, wordt een ringvorminge zonsverduistering als gedeeltelijk gezien.
Ringvormig-totale zonsverduistering (hybride): De afstand tussen de maan en de plek waar (het verlengde van) de kernschaduwkegel van de maan de aarde raakt, is gedurende de verduistering niet helemaal constant ten gevolge van de bolvorm van het aardoppervlak. Er is daarom een grensgeval mogelijk tussen een totale zonsverduistering en een ringvormige zonsverduistering waarbij de eclips gedurende een deel van haar duur totaal is en gedurende het andere deel ringvormig. Men spreekt dan van een ringvormig-totale zonsverduistering. Voor dergelijke eclipsen is het moeilijk zeer precies te bepalen waar zij overgaan van ringvormig naar totaal of omgekeerd, omdat hiervoor rekening moet worden gehouden met de preciese vorm van de aarde (die afwijkt van de bolvorm!) en van het reliëf.
Frequentie van zons- en maansverduisteringen
Om een totale of ringvormige zonsverduistering te kunnen hebben, moeten zon, maan en aarde in die volgorde precies op één lijn staan. Bekeken vanuit een geocentrisch standpunt is dit het geval als het nieuwe maan is én de maan in één van haar knopen staat of als het nieuwe maan is én de zon in één van de knopen van de maanbaan staat.
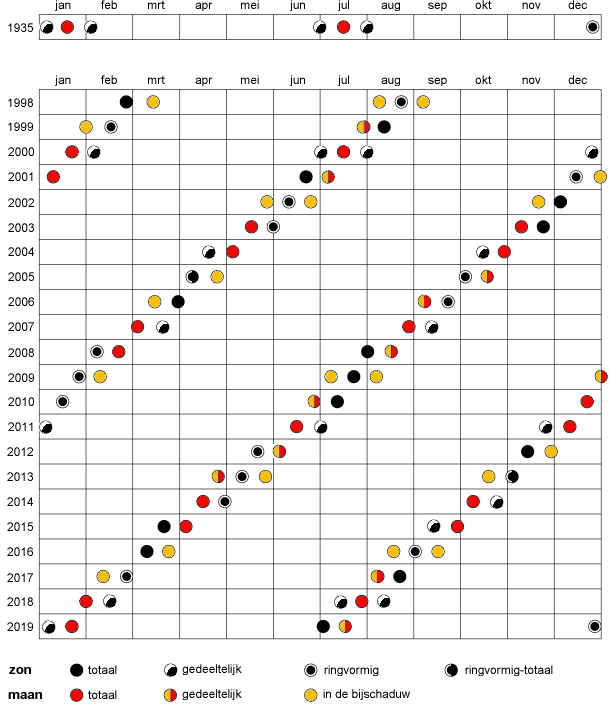
Bovenstaande figuur toont alle zons- en maansverduisteringen in de periode 1998-2019 op een schematische wijze die meteen de eclipsseizoenen zichtbaar maakt.
Gelukkig voor wie graag zonsverduisteringen ziet, is de aarde niet puntvormig. Daardoor kunnen bij nieuwe maan, ergens op aarde, zon, maan en waarnemer precies oplijnen als de zon in de buurt van een knoop staat. Als we gedeeltelijke zonsverduistering ook meerekenen, wordt de marge zelfs nog iets groter. Het tijdsinterval waarbinnen de zon dicht genoeg bij een knoop staat om bij nieuwe maan ergens op aarde een zonsverduistering te hebben, noemt men een eclipsseizoen. Een eclipsseizoen duurt ongeveer 37 dagen. In het midden ervan gaat de zon door een knoop van de maanbaan.
De meeste jaren tellen twee volledige eclipsseizoenen. Omdat één eclipsseizoen langer duurt dan één lunatie, valt er in elk eclipsseizoen minstens één nieuwe maan en dus zijn er elk jaar minstens twee zonsverduisteringen. Er kunnen echter ook twee nieuwe manen in een eclipsseizoenen vallen, waardoor er in een jaar ook vier zonsverduisteringen kunnen plaatsvinden.
Wat de figuur ook mooi illustreert, is het teruglopen van de eclipsseizoenen met ongeveer 19 dagen per jaar ten gevolge van de teruglopende beweging van de knopenlijn van de maanbaan met ongeveer 19° per jaar. Wanneer, zoals in 1935, het eerste eclipsseizoen aanvangt rond het begin van het jaar, zal het einde van het jaar nog het begin van een derde eclipsseizoen bevatten. Hierin kan nog een vijfde zonsverduistering optreden.
We concluderen dus dat er jaarlijks 2 tot 5 zonsverduisteringen plaatsvinden. Hoe groter het aantal eclipsen, hoe waarschijnlijker dat het om partiële gaat. In een eclipsseizoen met twee zonsverduisteringen moeten deze immers respectievelijk vroeg en laat in dat eclipsseizoen plaatsvinden, wanneer de zon al redelijk ver van de maanknoop verwijderd is. Tenslotte merken we nog op dat jaren met 5 zonsverduisteringen erg zeldzaam zijn. Het laatste dergelijke jaar was 1935; de eerstvolgende zijn 2206, 2709, 2774, 2839 en 2904.
Saros-reeksen
Zoals hierboven reeds opgemerkt, is een eclipsjaar (gemeten t.o.v. de knopenlijn van de maanbaan) ongeveer 19 dagen korter dan een siderisch jaar, ten gevolge van het teruglopen van de knopenlijn van de maanbaan. De duur van een eclipsjaar bedraagt ongeveer 346.62 dagen.
We merken nu de volgende merkwaardigheden op:
223 synodische maanden = 6585.32 dagen
242 draconitische maanden = 6585.36 dagen
19 eclipsjaren = 6585.78 dagen
239 anomalistische maanden = 6585.54 dagen
De periode van 6585.33 dagen, dit wil zeggen 18 jaar en 11.33 dagen of 10.33 dagen (afhankelijk van of er vier dan wel vijf schrikkeljaren in die periode vallen) noemt men een sarosperiode. Dit begrip was reeds bekend in de Oudheid: het woord "saros" is afgeleid van het Babylonische woord voor "periode".
Merkwaardig is dat een sarosperiode ongeveer gelijk is aan een geheel aantal synodische maanden, een geheel aantal draconitische maanden, een geheel aantal eclipsjaren en een geheel aantal anomalistische maanden; de preciese waarde van al deze veelvouden doet niet ter zake. Concreet heeft dit voor gevolg dat de omstandigheden die aanleiding geven tot een zonsverduistering zich na een sarosperiode vrij exact herhalen, tot zelfs de afstand aarde-maan toe, belangrijk om te beoordelen of een niet-gedeeltelijke verduistering totaal of ringvormig is en zo ja, hoe lang de totale of ringvormige fase duurt!
Door de kleine verschillen in de bovenstaande tabel, duurt een sarosreeks (een rij zonsverduisteringen met telkens een sarosperiode tussen) niet onbeperkt lang, maar gemiddeld 1350 jaar. Ze telt typisch 75 eclipsen.
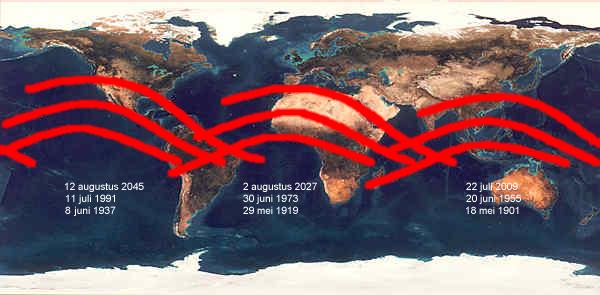
Een reeks zonsverduisteringen van saros 136. Merk op hoe opeenvolgende verduisteringen van dezelfde sarosreeks inderdaad telkens 120° verder plaatsvinden, en mooi 18 jaar en 10 à 11 dagen na mekaar plaatsvinden.
Tenslotte merken we nog op dat de fractie van een derde dag in de sarosperiode voor gevolg heeft dat het zichtbaarheidsgebied van een zonsverduistering telkens 120° verschuift op het aardoppervlak, waardoor we na drie sariosperiodes terug een eclips in hetzelfde gebied van de wereld krijgen. Onderstaande figuur illustreert dit zeer mooi.